Disentangling Disentanglement: how VAEs learn Independent Components

This post summarises Unpicking Data at the Seams: VAEs, Disentanglement and Independent Components (Allen, 2024), which explains why disentanglement arises in generative latent variable models.

Disentanglement is an intriguing phenomenon observed in generative latent variable models, such as Variational Autoencoders (VAEs) (our focus), Generative Adversarial Networks (GANs) and latent Diffusion models. Although disentanglement has not been rigorously defined, it refers to when semantically meaningful factors of the data map to distinct dimensions in latent space. This allows, for example, images to be generated that vary by a particular feature by changing a single latent dimension (Figure 1 (left), or this video on disentanglement in GANs). It also allows apparent “embedding arithmetic”, e.g. the vector difference between embeddings of two images that vary in style can be added to that of a third image to transform its style (Figure 1, right).

While disentanglement is often associated with particular model families whose popularity may ebb and flow (e.g. VAEs, $\beta$-VAEs, GANs), we show that the phenomenon itself relates to the latent structure of the data and is more fundamental than any model that may expose it.

Figure 1. Illustrating disentanglement: (left) Each row of images varies by a single semantic feature, e.g. hair style or orientation. Disentanglement means that (i) such images can be generated by varying a _single_ latent dimension, i.e. by traversing the latent space in "axis-aligned" directions (parallel to standard basis vectors); and (ii) each latent variable affects a distinct semantic feature rather than several or all. (right) Changing the style of an image in diffusion models by disentangled features. (Images from Voynov & Babenko (2020) and Wu et al. (2023))

$\bullet$ Motivation: Disentanglement is particularly intriguing because models such as VAEs are not intentionally designed to achieve it, and it even occurs in settings impossible for other methods (i.e. isotropic Gaussian prior).¹$^,$² Thus understanding disentanglement may provide new insights into how models learn and what is learnable. More broadly, the ability to separate out independent aspects of the data is relevant to many areas of machine learning, and teasing its generative factors apart may offer fundamental insights into the data itself.

Machine learning has made incredible breakthroughs in recent years but our theoretical understanding lags notably behind, which may have serious implications as models increasingly reach the public sphere. Thus, a fundamental motivation for this work is to unravel some of the mystery of machine learning. We re-emphasise that disentanglement is not a model feature, rather a property of the data that a model may or may not expose and so is of more general interest. That said, autoencoding the data is often the first step in latent diffusion models, so understanding the latent space is relevant to current state of the art models.

$\bullet$ Approach: Recent works suggest that disentanglement arises in VAEs because commonly used diagonal posterior covariance matrices promote column-orthogonality in the decoder’s Jacobian.³$^,$⁴ In empirical support, columns of the decoder Jacobian are indeed found to be closer to orthogonal in VAEs with diagonal covariance than those with full covariance or general auto-encoders;³ and directly encouraging column-orthogonality with a constraint is shown to induce disentanglement.⁴

Building on this, Allen (2024): (A) further clarifies the connection between diagonal covariance and Jacobian orthogonality and (B) explains how disentanglement follows, showing that it amounts to factorising the data distribution into statistically independent components.

$$ \begin{equation} \text{diag. posterior covariance} \quad \overset{A}{\Rightarrow}\quad \text{column-orthog. Jacobian} \quad \overset{B}{\Rightarrow}\quad \text{disentanglement} \end{equation} $$

$\bullet$ Problem set-up: As in a VAE (or GAN), we assume that data $x\in\mathcal{X} \subseteq\mathbb{R}^n$ are generated by a latent variable model: independent latent variables are sampled $z\in\mathcal{Z} =\mathbb{R}^m$, $p(z) = \prod_ip(z_i)$, and mapped stochastically to the data space by sampling $x\sim p(x\mid z)$. The latent prior is commonly assumed to be isotropically Gaussian $p_\theta(z_i) = \mathcal{N}(z_i,0,1)$. We also assume $p_\theta(x\mid z)$ is Gaussian. [Notation: unsubscripted probability distributions denote the ground truth; subscripts indicate modelled distribution.]

TL;DR:

Disentanglement provably occurs in the linear case, $p_\theta(x\mid z) = \mathcal{N}(x; Dz,\sigma^2I),\ D\in\mathbb{R}^{n\times m}$, corresponding to probabilistic PCA (PPCA). Of the infinite set of known solutions, a VAE with diagonal posterior covariance finds only those in which latent dimensions $z_i$ map to independent factors of variation in the data distribution, which defines disentanglement.
Surprisingly, the rationale for the linear case (described later in this post) extends to non-linear VAEs with diagonal posterior covariance. The latter property encourages columns of the decoder’s Jacobian to be (approximately) orthogonal, which in turn means independent latent variables $z_i$ pass through the decoder and emerge (in $\mathcal{X}$) as statistically independent components that factorise the full push-forward distribution over the decoder-defined manifold.
- i.e. diagonal covariances cause the decoder to map independent factors in the latent space to independent components in the data space.
A VAE’s objective is maximised if the model distribution matches that of the data, hence if the data distribution factorises into independent components then the model distribution must similarly factorise. So independent factors of the data align with independent factors of the model, which (approximately) align with latent variables $z_i$ (from 2.) and so independent factors of $p(x)$ map to distinct latent variables of the model, i.e. $p(x)$ is disentangled.

$$ \begin{equation} \text{diag. posterior covariance} \quad \overset{A}{\Rightarrow}\quad \text{column-orthog. Jacobian} \color{lightgray}{\quad \overset{B}{\Rightarrow}\quad \text{disentanglement}} \end{equation} $$

(A) From Diagonal Covariance to Jacobian Orthogonality

The VAE fits a latent variable model $p_\theta(x) =\int_z p_\theta(x\mid z)p_\theta(z)$ to the data distribution $p(x)$ by maximising the Evidence Lower Bound (ELBO),

\[\ell(\theta, \phi) \quad =\quad \int p(x) \int q_\phi(z\mid x) \ \{\ \log p_\theta(x\mid z) \,-\, \beta \log \tfrac{q_\phi(z\mid x)}{p_\theta(z)} \ \}\ dz dx\ ,\]

where the ELBO has $\beta=1$ and $\beta>1$ is found to improve disentanglement. We assume common VAE assumptions:

$p_\theta(x\mid z) =\mathcal{N}(x;\,d(x),\sigma^2)\quad$ with decoder $d\in\mathcal{C}^2$ (injective) and fixed variance $\sigma^2$;
$q_\phi(z\mid x)=\mathcal{N}(z;\,e(x),\Sigma_x)\quad$ with encoder $e$ and learned variance $\Sigma_x$; and
$p_\theta(z)\quad\ \ \ =\mathcal{N}(z;\,0,I)\quad$ where $z_i$ are independent with $p_\theta(z_i)=\mathcal{N}(z_i;0,1)$.

Maximising the ELBO = maximum-likelihood$^{++}$: Maximising the likelihood $\int p(x)\log p_\theta(x)$ minimises the KL divergence between the data and model distributions, but this is often intractable for a latent variable model. Maximising the ELBO minimises the KL divergences between $p(x)q_\phi(z\mid x)$ and $p_\theta(x)p_\theta(z\mid x)\doteq p_\theta(x\mid z)p_\theta(z)$, aligning two models of the joint distribution.

The ELBO is optimised when $\Sigma_x$ relates to the Hessian of $\log p_\theta(x\mid z)$ (Opper & Archambeau) hence under certain conditions⁵ when:

\[\begin{equation} \Sigma_x^{-1} \ \ \overset{O\&A}{=}\ \ I - \mathbb{E}_{q(z\mid x)}[\tfrac{\partial^2\log p_\theta(x\mid z)}{\partial z_i\partial z_j}] \ \ \approx\ \ I + \mathbb{E}_{q(z\mid x)}[\tfrac{1}{\beta\sigma^2}J_z^\top J_z]\ , \tag{1}\label{eq:one} \end{equation}\]

where $J_z$ is the Jacobian of $d$ evaluated at $z$. For this to hold with diagonal $\Sigma_x$, columns of $J_z$ must be (approximately) orthogonal, $\forall z$.⁶ If $J_z=U_zS_zV_z^\top$ is the singular value decomposition (SVD), then $J_z$ is column-orthogonal $\quad$ iff $\ \ J_z^\top J_z = V_zS_z^2V_z^\top$ is diagonal $\quad$ iff $\ \ V_z=I$. Hence, by the definition of the Jacobian, diagonal covariances mean that perturbations in latent space in standard basis vectors $z_i$ (right singular vectors of $J_z$) correspond to perturbations in data space in directions $\mathbf{u}_i$ (column $i$ of $U_z$, left singular vectors of $J_z$), with no effect in any other $\mathbf{u}_{j\ne i}$. Note that this singles out axis-aligned directions in the latent space as “special”, breaking the rotational symmetry implied by the Gaussian prior.

Take-away: the ELBO is maximised as approximate posterior covariances $\Sigma_x$ tend to optimal posterior covariances defined by derivatives of $\log p_\theta(x\mid z)$. Diagonal covariances do not necessarily imply column-orthogonality in the decoder Jacobian, but if they exist, the VAE looks for solutions where the Hessian is diagonal hence where columns of the Jacobian are ($\approx$) orthogonal.

$$ \begin{equation} {\color{lightgray}{\text{diag. posterior covariance} \quad \overset{A}{\Rightarrow}}}\quad \text{column-orthog. Jacobian} \quad \overset{B}{\Rightarrow}\quad \text{disentanglement} \end{equation} $$

(B) From Orthogonality to Statistical Independence

Understanding that diagonal posterior covariance promotes column-orthogonality in the decoder Jacobian, the question then is how does that geometric property leads to the statistical property of disentanglement. For that we consider the push-forward distribution defined by the decoder, supported over a $m$-dimensional manifold $\mathcal{M}_d\subseteq\mathcal{X}$.

A push-forward distribution describes the probability distribution of the output of a deterministic function given an input distribution. A VAE decoder maps samples of the latent prior $p_\theta(z)$ to the data space, where it defines a manifold $\mathcal{M}_d$ and push-forward distribution over it.

Linear Case

For intuition, we first consider the linear case $x=d(z)=Dz$, $D\in\mathbb{R}^{n\times m}$, the model considered in Probabilistic PCA (PPCA), which has a tractable MLE solution and known optimal posterior

\[\begin{equation} p_\theta(z\mid x) = \mathcal{N}(z;\, \tfrac{1}{\sigma^2}M D^\top x,\, M) \quad\quad\quad M = (I + \tfrac{1}{\sigma^2}D^\top D)^{-1} \tag{2}\label{eq:two} \end{equation}\]

Since $D$ is the Jacobian of $d$, the latter expression is in fact a special case of \eqref{eq:one}. Hence if $D=USV^\top$ is the SVD, the ELBO is maximised when $\Sigma_x=M,\ \forall x\in\mathcal{X}$ and so, for diagonal $\Sigma_x$, when $V=I$.

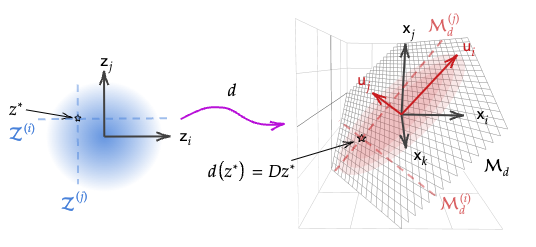linear2 Figure 2. Illustration of linear decoder $d:\mathcal{X}\to\mathcal{Z}$. The latent Gaussian prior is mapped to a Gaussian distribution in the data space over a linear manifold.

The aim is to understand how that constraint affects how independent dimensions $z_i\in\mathcal{Z}$ and the probability density over them pass through the decoder. For a given point $z^*\in \mathcal{Z}$, let:

$\mathcal{Z^{(i)}}\subset\mathcal{Z}$ be lines passing through $z^*$ parallel to each standard basis vector $e_i$ (blue dashed lines in Fig. 2), and $\mathcal{M}_d^{(i)}\subset\mathcal{M_d}$ be their images under $d$ that follow $\mathbf{u}_i$, the left singular vectors of $D$ (red dashed lines); and
$x^{(U)}=U^\top x=U^\top Dz^*$ be $x$ in the basis defined by columns of $U$⁷

Crucially, the Jacobian of the map from $z$ to $x^{(U)}$ is the diagonal matrix $S$, i.e. $\tfrac{\partial x^{(U)}_i}{\partial z_j} =\{s_i\doteq S_{i,i} \text{ if }i=j; 0 \text{ o/w}\}$. It then follows that independent $z_i$ map to independent components $x^{(U)}_i$ since:

each $x^{(U)}_i$ varies only with a distinct $z_i$ by considering $\tfrac{\partial x^{(U)}_i}{\partial z_j}$ and so are independent;
the push-forward of $d$ restricted to $\mathcal{Z^{(i)}}$ has density $p(x^{(U)}_i) = \mid\! s_i\!\mid ^{-1}p(z_i)$ over $\mathcal{M}_d^{(i)}$; and
the full push-forward distribution is $p(Dz) = \mid\!D\!\mid ^{-1}p(z) = \prod_i \mid\! s_i\!\mid^{-1}p(z_i) = \prod _ip(x^{(U)}_i)$.

This shows that the push-forward distribution defined by the decoder factorises as a product of independent univariate distributions $p(x^{(U)}_i)$, which each correspond to a distinct latent dimension $z_i$. Thus, if the data follows that generative process and so factorises (with factors determined by the SVD of ground truth $D$), then the ELBO is maximised when independent factors of the model align with those of the data and so p(x) is disentangled as a product of independent components that align with latent dimensions.

This may not seem a surprise in the linear case since it is known from the outset that the push-forward distribution is Gaussian and so factorises as a product of univariate Gaussians. However, neither that fact nor the linearity of $d$ was used at any stage.

Non-linear Case with Diagonal Jacobian

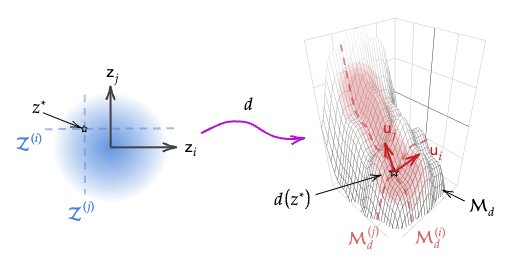non_linear2 Figure 3. Illustration of non-linear decoder $d:\mathcal{X}\to\mathcal{Z}$. The latent Gaussian prior is mapped to a push-forward distribution in the data space over a non-linear manifold.

We now take an analogous approach for a general VAE ($x=d(z)$, $d\in\mathcal{C}^2$) with column-orthogonal decoder Jacobian. The Jacobian and its factors, $J_z=U_zS_zV_z^\top$, may now vary with $z$, however column-orthogonality restricts $V_z=I,\ \forall z\in \mathcal{Z}$ and $U_z$, $S_z$ are continuous w.r.t. $z$ (from $d\in\mathcal{C}^2$ and Papadopoulo & Lourakis (2006)).

As in the linear case, for any $z^*\in \mathcal{Z}$, we can define lines $\mathcal{Z^{(i)}}\subset\mathcal{Z}$ passing through $z^*$ parallel to the standard basis (blue dashed lines in Fig. 3), and their images under $d$, $\mathcal{M}_d^{(i)}\subset\mathcal{M_d}$, which are potentially curved sub-manifolds following (local) left singular vectors of $J_{z^*}$ (red dashed lines).

Considering $x=d(z)$ in the local $U$-basis (i.e. columns of $U_z$), denoted $x^{(U)}=U_z^\top x$, the Jacobian of the map from $z$ to $U_z^\top x^{(U)}$ is again diagonal $S_z$. Hence, as in the linear case, independent $z_i\in\mathcal{Z}$ map to independent components $x^{(U)}_i$ and:

$\{x^{(U)}_i\}_i$ are independent (by consideration of partial derivatives $\tfrac{\partial x^{(U)}_i}{\partial z_j}$);
the push-forward of $d$ restricted to $\mathcal{Z^{(i)}}$ has density $p(x^{(U)}_i) = \mid\! s_i\!\mid^{-1}p(z_i)$ over $\mathcal{M}_d^{(i)}$; and
the full push-forward satisfies $p(d(z)) = \mid J_z\mid ^{-1}p(z) = \prod_i \mid\! s_i\!\mid^{-1}p(z_i) = \prod _ip(x^{(U)}_i)$.

Thus, by the same argument as in the linear case, the distribution over the decoder manifold factorises as a product of independent univariate push-forward distributions $p(x^{(U)}_i)$, each corresponding to a distinct latent dimension $z_i$.

Putting everything together:

The ELBO is maximised if the model distribution fits the data distribution, so assuming that the data distribution has independent factors (by being generated under the considered model or otherwise) the model distribution must factorise similarly.
From part A, diagonal covariance matrices encourage the decoder’s Jacobian to be (approximately) column-orthogonal and, where so, the push-forward distribution over the model manifold factorises into components aligned with latent dimensions (from part B).
Thus the ELBO is maximised if independent components of the data distribution align with those of the model and if those of the model align with latent dimensions, thus the VAE aligns independent components that factorise the data distribution with latent dimensions, which defines disentanglement.
- (Identifiability depends on uniqueness of independent component distributions, analogous to uniqueness of singular values in the linear case).

Key insight: the above result hinges on the SVD of the Jacobian $J_z = U_zS_zV_z^\top$. By differentiability of $d$, the bases defined by columns of $U_z$ and $V_z$ (in $\mathcal{X}$ and $\mathcal{Z}$ resp.) are continuous in $z$ so basis vectors form continuous curves in each domain (these are linear in $\mathcal{Z}$ when $V_z=I$). By definition of the SVD, traversing a submanifold in one domain corresponds to traversing a corresponding submanifold in the other and the mapping between $x$ considered in the $U$-basis and $z$ considered in the $V$ basis has diagonal Jacobian given by $S_z$ - irrespective of how complex $d$ may be, whether a single linear layer or a thousand-layer CNN! As such, probability densities over submanifolds in $\mathcal{Z}$ map separably to their counterpart in $\mathcal{X}$, which is to say, independent components in $\mathcal{Z}$ map to independent components in $\mathcal{X}$.

Notes:

While we assume $d\in\mathcal{C^2}$, i.e. differentiability, the result also holds for continuous $d\in\mathcal{C^1}$ differentiable almost everywhere, e.g. ReLU networks.
We recommend reading the full paper for further details, such as:
- consideration of whether orthogonality is strictly necessary for disentanglement (the argument above shows it is sufficient);
- further consideration of model identifiability, i.e. up to what symmetries a VAE can identify ground truth generative factors; and
- explanation of the role of $\beta$ in a $\beta$-VAE, notably:
  - if $p_\theta(x\mid z)$ is of exponential family form then $\beta$ corresponds to Var$_\theta[x\mid z]$ (generalising $\sigma^2$ in the Gaussian case); and
  - $\beta$ acts a “glue” determining how close data points need to be (in Euclidean norm) for the model to treat them as “similar”, i.e. for their representations to merge.

Final remarks

We hope this post provides clearer insight into (i) what disentanglement means and how diagonal covariances, a seemingly innocuous design choice motivated by computational efficiency, leads to it; (ii) how statistically independent components of the data form “seams” running through the data manifold, which a VAE tries to “unpick”; and (iii) how understanding may transfer surprisingly well from linear to non-linear models.

This work throws up many interesting questions, e.g.:

if the VAE objective aims to disentangle, why is disentanglement not observed more reliably, e.g. as observed by Locatello et al. (2019)?
how does this relate to VAE extensions that enhance entanglement, such as FactorVAE and TC-VAE?
can this be used to automatically identify independent factors in the latent space of other models, e.g. GANs and latent diffusion models?
since this result is for continuous data domains, does it translate to discrete data such as text?
what does this insight into the structure of the data mean for other modelling paradigms, e.g. supervised, semi-supervised, self-supervised and reinforcement learning?

If any of these or related questions are of interest and you would like to collaborate, please free to get in touch (by email, twitter or bluesky).

Thanks for reading! We welcome any constructive feedback or discussion on this post on bluesky (I have pinned a link @carl-allen.bsky.social).

Challenging Common Assumptions in the Unsupervised Learning of Disentangled Representations; Locatello et al. (2019) ↩
Variational Autoencoders and Nonlinear ICA: A Unifying Framework; Khemakhem et al. (2020) ↩
Variational Autoencoders Pursue PCA Directions (by Accident); Rolinek et al. (2019) ↩ ↩²
On Implicit Regularization in β-VAEs; Kumar \& Poole (2020) ↩ ↩²
When second derivatives of the decoder are small almost everywhere, e.g. as in ReLU networks (see Abhishek & Kumar, 2020). ↩
As previously suggested more additional approximation steps and assumptions.³$^,$⁴ ↩
Note that we use slightly different notation to the original paper. ↩